广度优先搜索原理与实践深度优先搜索原理与实践（java

概论

在 深度优先搜索原理与实践（java）文章介绍了深度优先搜索算法的理论和实践。本文将介绍与其原理类似的广度优先搜索算法。

广度优先搜索（也称宽度优先搜索，缩写 BFS，以下采用广度来描述）是连通图的一种遍历算法这一算法也是很多重要的图的算法的原型。Dijkstra 单源最短路径算法和 Prim 最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫 BFS，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。基本过程，BFS 是从根节点开始，沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问，则算法中止。一般用队列数据结构来辅助实现 BFS 算法。

基本原理

对于下面的树而言，BFS 方法首先从根节点1开始，其搜索节点顺序是 1,2,3,4,5,6,7,8。

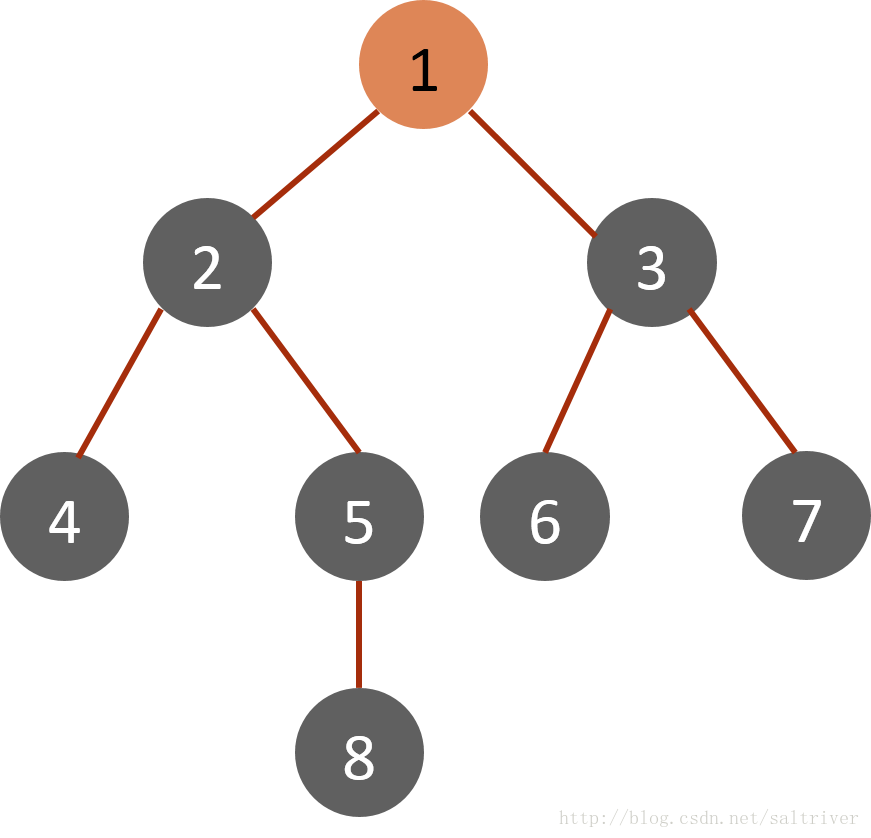
BFS 使用队列 (queue) 来实施算法过程，队列 (queue) 有着先进先出 FIFO (First Input First Output)的特性，

BFS 操作步骤如下：

把起始点放入 queue；
重复下述2步骤，直到 queue 为空为止：

- 从queue中取出队列头的点；

- 找出与此点邻接的且尚未遍历的点，进行标记，然后全部放入queue中。

下面结合一个图 (graph) 的实例，说明 BFS 的工作过程和原理：
（1）将起始节点1放入队列中，标记为已遍历：

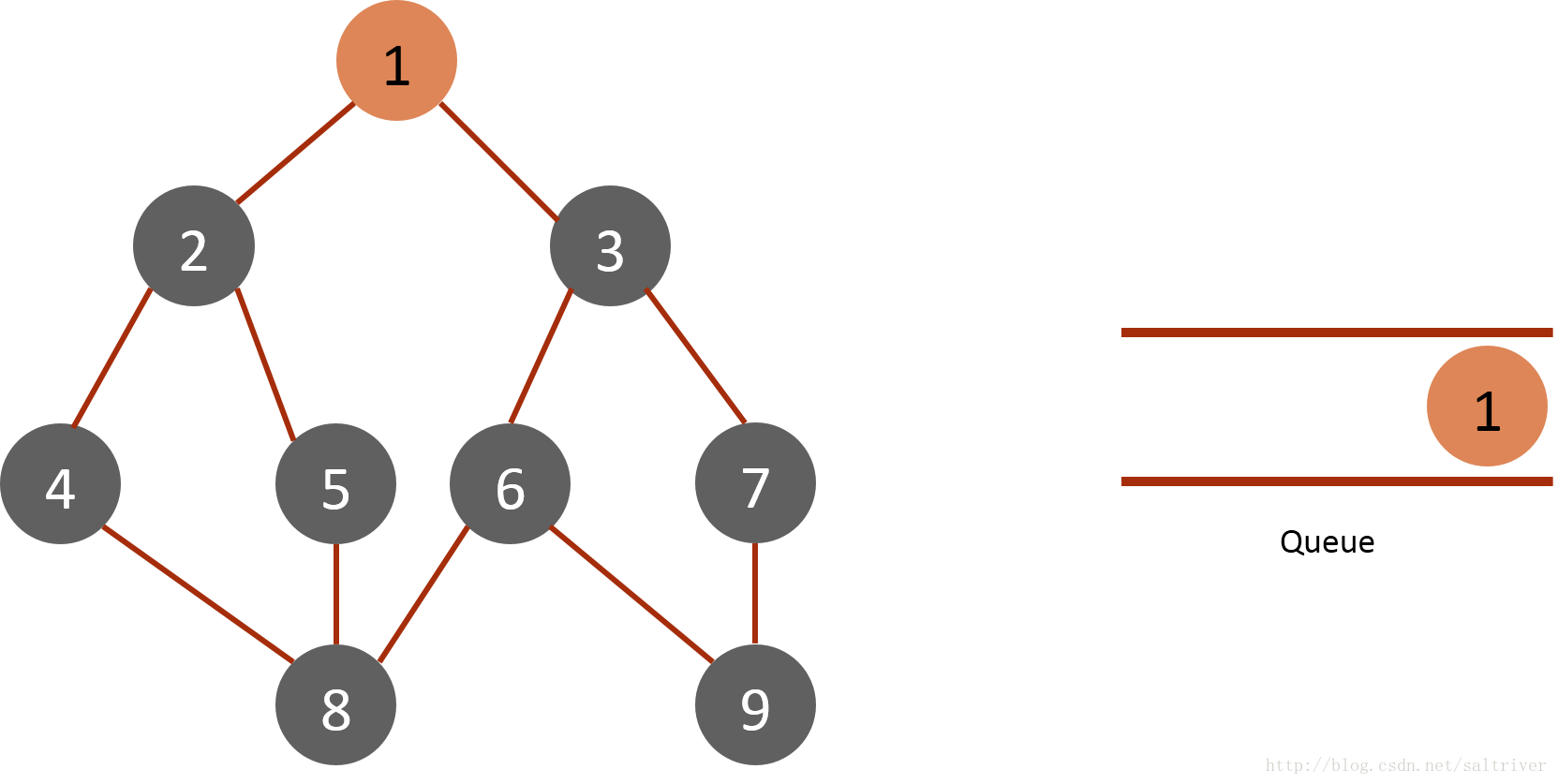
（2）从queue中取出队列头的节点1，找出与节点1邻接的节点2,3，标记为已遍历，然后放入queue中。

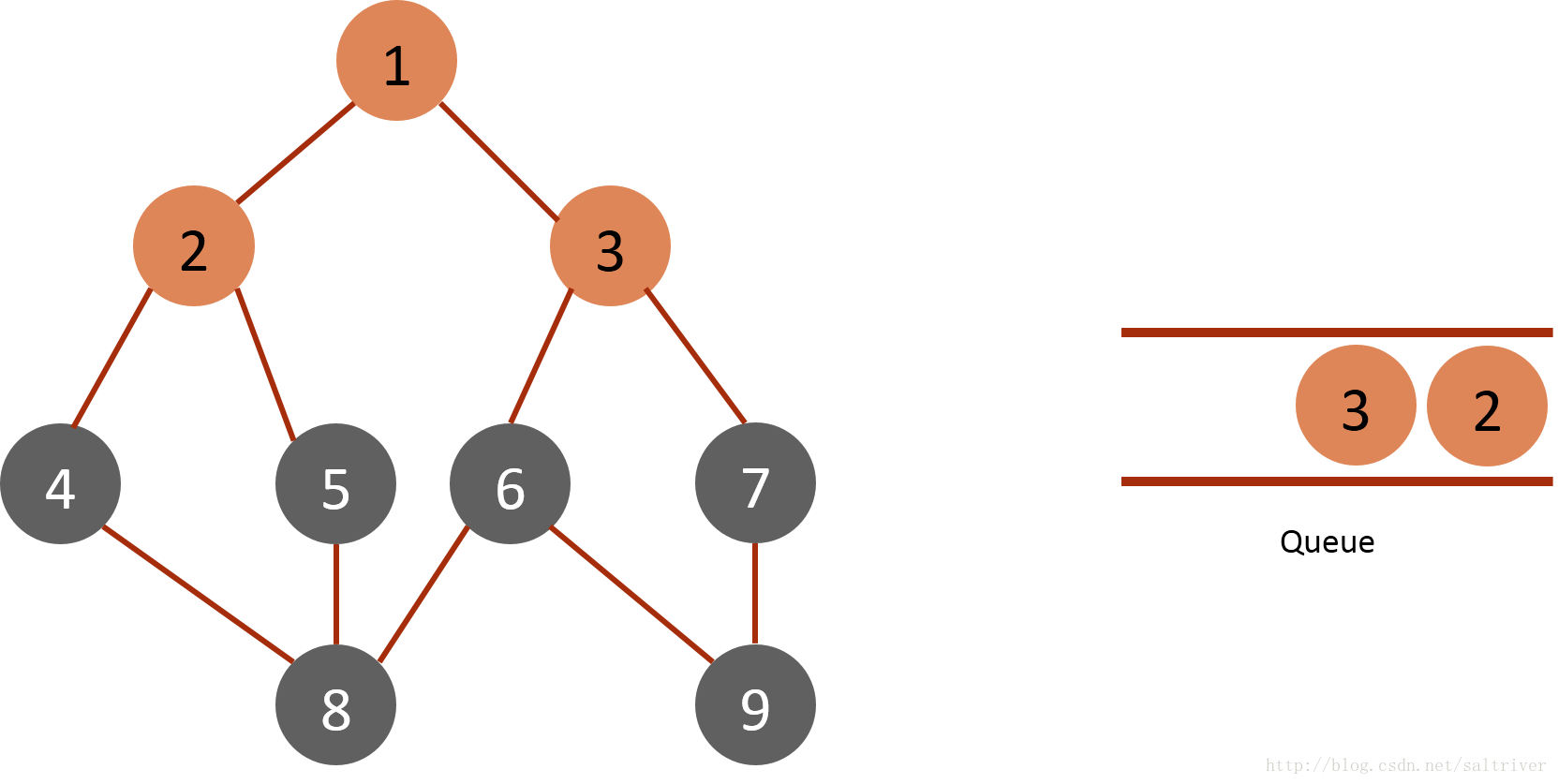
（3）从queue中取出队列头的节点2，找出与节点2邻接的节点1,5，由于节点1已遍历，排除；标记4,5为已遍历，然后放入queue中。

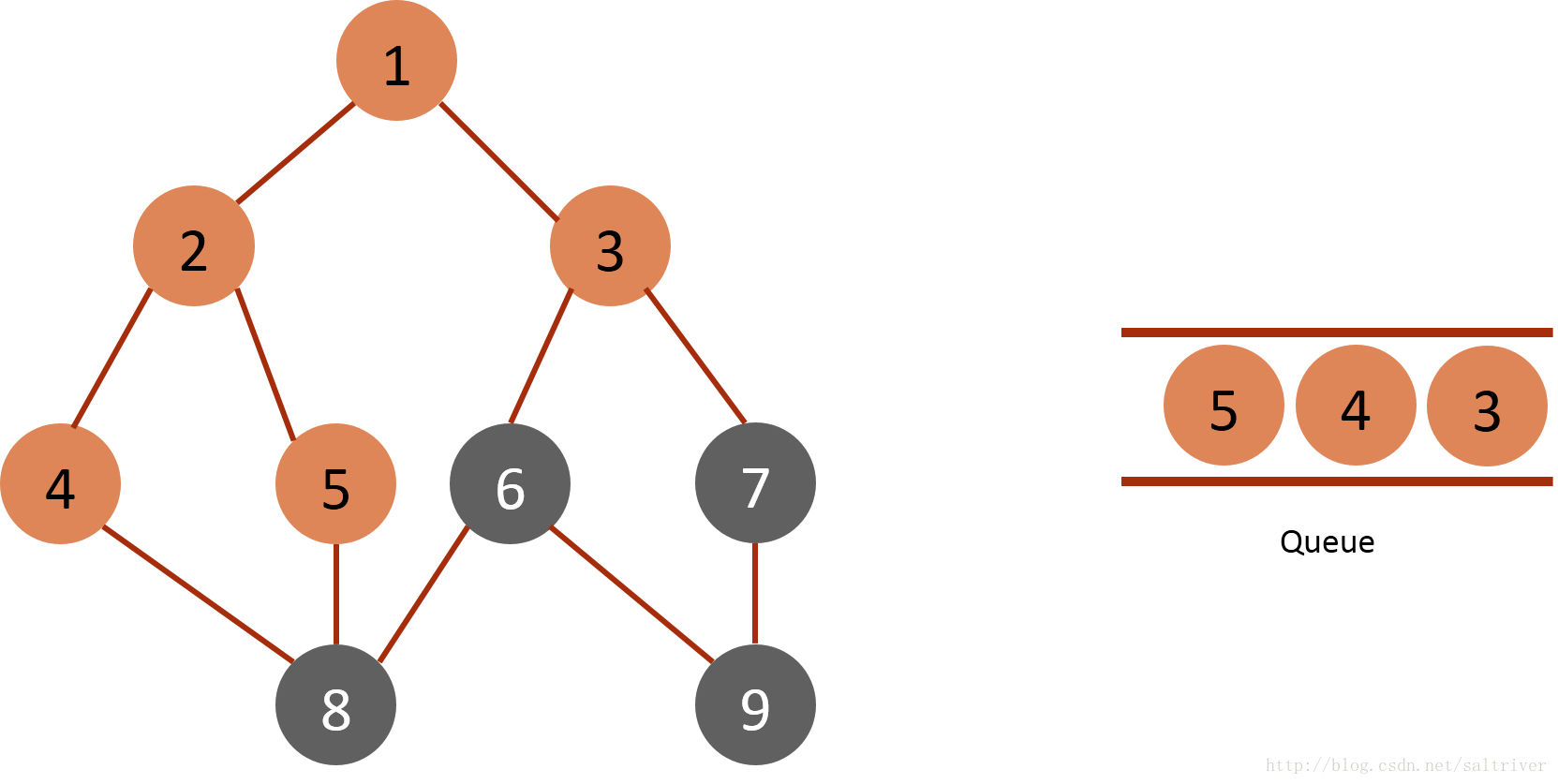
（4）从queue中取出队列头的节点3，找出与节点3邻接的节点1,7，由于节点1已遍历，排除；标记6,7为已遍历，然后放入queue中。

（5）从queue中取出队列头的节点4，找出与节点4邻接的节点2,8，2属于已遍历点，排除；因此标记节点8为已遍历，然后放入queue中。

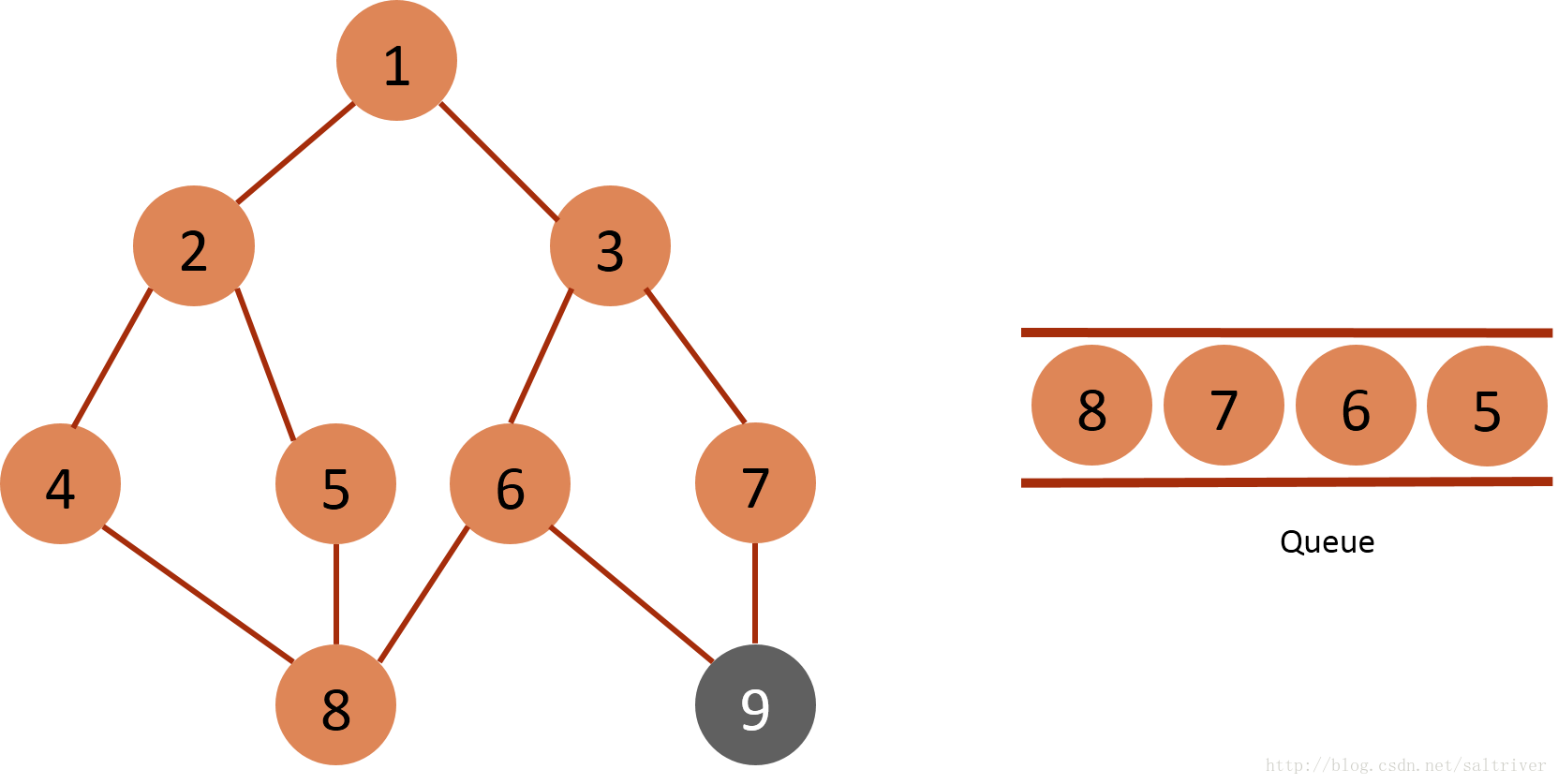
（6）从queue中取出队列头的节点5，找出与节点5邻接的节点2,8，2,8均属于已遍历点，不作下一步操作。

（7）从queue中取出队列头的节点6，找出与节点6邻接的节点3,8,9，3,8属于已遍历点，排除；因此标记节点9为已遍历，然后放入queue中。

（8）从queue中取出队列头的节点7，找出与节点7邻接的节点3,9属于已遍历点，不作下一步操作。

（9）从queue中取出队列头的节点8，找出与节点8邻接的节点4,6，4,6属于已遍历点，不作下一步操作。

（10）从queue中取出队列头的节点9，找出与节点9邻接的节点6,7，6,7属于已遍历点，不作下一步操作。

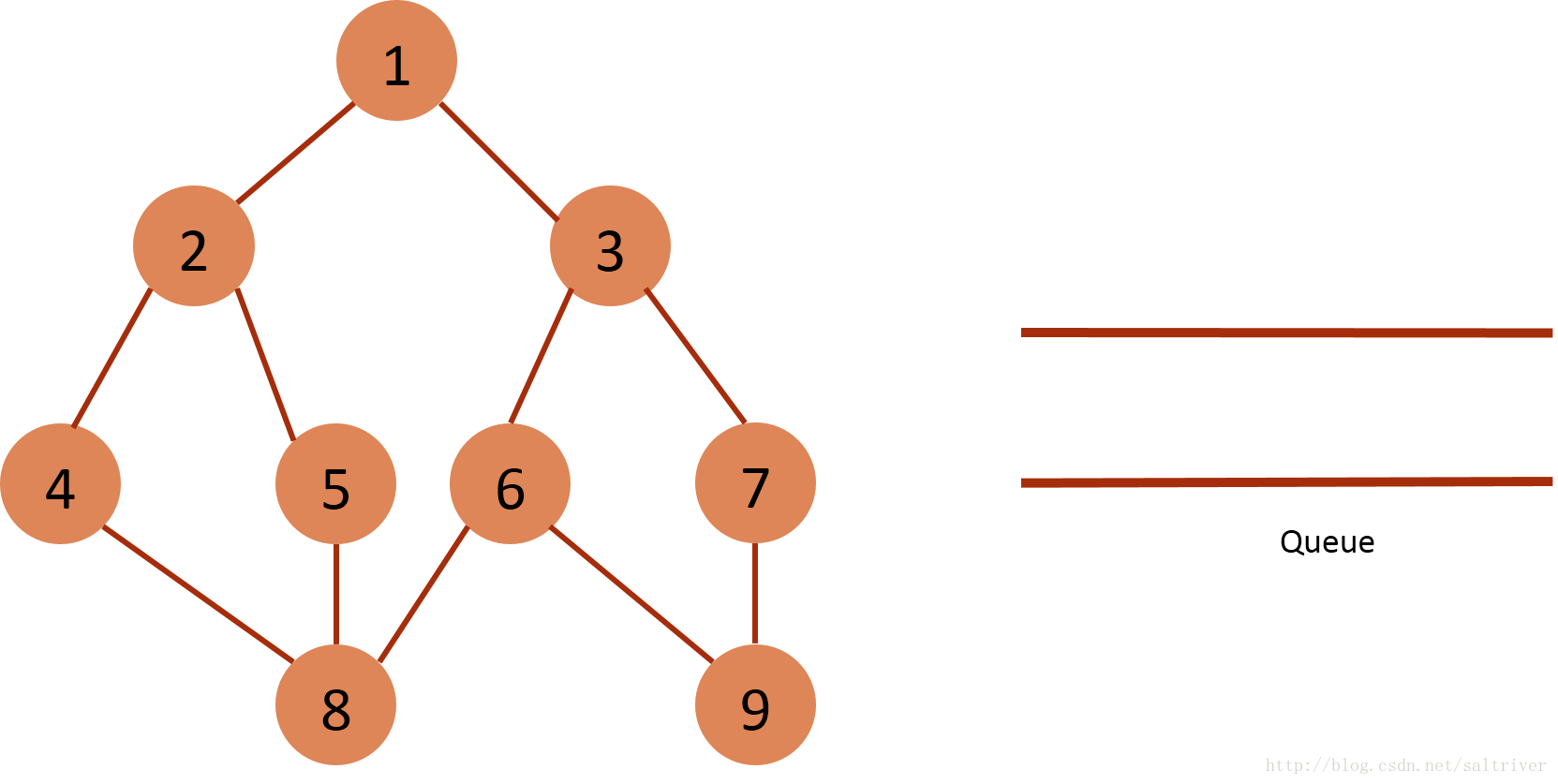
（11）queue 为空，则遍历结束

上面过程可以用下面的代码来表示：

    private Map<String,Boolean> status = @H_403_136@new HashMap<String,Boolean>@H_403_136@();
    @H_403_136@private Queue<String> queue = @H_403_136@new LinkedList<String>@H_403_136@public @H_403_136@void@H_403_136@ BFSSearch(String startPoint) {
        //@H_403_136@1.把起始点放入queue；
@H_403_136@        queue.add(startPoint);
        status.put(startPoint,@H_403_136@false@H_403_136@);
        bfsLoop();
    }
    
    @H_403_136@private @H_403_136@ bfsLoop() {
        @H_403_136@while(!@H_403_136@queue.isEmpty()) {
            @H_403_136@  1) 从queue中取出队列头的点；更新状态为已经遍历。
            String currentQueueHeader = queue.poll(); @H_403_136@出队
            status.put(currentQueueHeader,@H_403_136@true@H_403_136@);
            System.out.println(currentQueueHeader);
            @H_403_136@  2) 找出与此点邻接的且尚未遍历的点，进行标记，然后全部放入queue中。
            List<String> neighborPoints =@H_403_136@ graph.get(currentQueueHeader);
            @H_403_136@for@H_403_136@ (String poinit : neighborPoints) {
                @H_403_136@if (!status.getOrDefault(poinit,1)">false)) { @H_403_136@未被遍历
                    @H_403_136@if (queue.contains(poinit)) @H_403_136@continue@H_403_136@;
                    queue.add(poinit);
                    status.put(poinit,1)">);
                }
            }
        }
    }

通用框架

@H_403_136@@H_403_136@其通用框架可以概括为：

@H_403_136@ bfs(起始点) {
    将起始点放入队列中;
    标记起点访问;
    @H_403_136@while@H_403_136@ (如果队列不为空) {  @H_403_136@// 一般采用while ，当然也可以使用递归
        访问队列中队首元素x;
        删除队首元素;
        @H_403_136@ (x 所有相邻点) {
            @H_403_136@if@H_403_136@ (该点未被访问过且合法) {
                将该点加入队列末尾;
            　　@H_403_136@  (该结点是目标状态) { @H_403_136@ // 达到目标，提前结束终止循环
                    置 flag= @H_403_136@true;    
@H_403_136@　　　　　　　　　　　　break@H_403_136@; 
               }
            }
        }
    }
    队列为空，广搜结束;
}

下面来总结下写出 BFS 算法规则：

通过这个 bfs 框架可以看出该方法主要有以下几个规律：

起点条件。从哪个点开始访问？是否每个点都需要当作起点？第一次 bfs 调用至关重要。
邻接点。如何去获取邻接点？通过起点可到达的点。如何保存邻接点？先进先出。一般采用队列。
循环参数。队列不为空。一个点的所有邻接点都是在一个 while 里面进行添加的，才会进入
访问标志。为了避免重复访问，需要对已经访问过的节点加上标记，避免重复访问。

讲完了理论，下面开始进入实战。

200. 岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1:

// 输入:
11110
11010
11000
00000
// 输出: 1

示例 2:

// 输入:
11000
11000
00100
00011
// 输出: 3

解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。

题目解答如下：

@H_403_136@class@H_403_136@ Solution {
    @H_403_136@int numIslands(@H_403_136@char@H_403_136@[][] grid) {
        @H_403_136@if (grid == @H_403_136@null || grid.length < 1 || grid[0].length<1@H_403_136@) {
            @H_403_136@return 0@H_403_136@;
        }
        @H_403_136@int num = 0@H_403_136@;
        @H_403_136@int nr =@H_403_136@ grid.length;
        @H_403_136@int nc = grid[0@H_403_136@].length;
@H_403_136@　　　　　// 每个点都可能是起点
        @H_403_136@for (@H_403_136@int x =0;x<nr;x++@H_403_136@int y =0;y<nc;y++@H_403_136@) {
                @H_403_136@if (grid[x][y]=='1'@H_403_136@) {
                    bfs(grid,x,y);
                    num++@H_403_136@;
                }
            }
        }
        @H_403_136@return@H_403_136@ num;
        
    }
@H_403_136@　　 // 对于 bfs 来说，只要队列不为空，就可以一直走到头,@H_403_136@void bfs(@H_403_136@char[][] grid,1)">int r,1)">int@H_403_136@ c) {
        @H_403_136@　　　　  // 队列，用于保存邻接点
        Queue<Integer> neighbors = @H_403_136@new LinkedList<>@H_403_136@();
@H_403_136@　　　　　// 这里可以学下，对于二维可以将坐标转化为一个数字
        neighbors.add(r * nc +@H_403_136@ c); 
        @H_403_136@while (!@H_403_136@neighbors.isEmpty()) {
@H_403_136@　　　　　　　// 每次循环开始的时候，需要移出一个点
            @H_403_136@int id =@H_403_136@ neighbors.remove();
            @H_403_136@int row = id /@H_403_136@ nc;
            @H_403_136@int col = id %@H_403_136@ nc;
@H_403_136@　　　　　　　// 四个邻接点都是在一个while循环里的
            @H_403_136@if (row - 1 >= 0 && grid[row-1][col] == '1'@H_403_136@) {
                neighbors.add((row-1) * nc +@H_403_136@ col);
                grid[row-1][col] = '0'@H_403_136@;
            }
            @H_403_136@if (row + 1 < nr && grid[row+1][col] == '1'@H_403_136@) {
                neighbors.add((row+1) * nc +@H_403_136@ col);
                grid[row+1][col] = '0'@H_403_136@if (col - 1 >= 0 && grid[row][col-1] == '1'@H_403_136@) {
                neighbors.add(row * nc + col-1@H_403_136@);
                grid[row][col-1] = '0'@H_403_136@if (col + 1 < nc && grid[row][col+1] == '1'@H_403_136@) {
                neighbors.add(row * nc + col+1@H_403_136@);
                grid[row][col+1] = '0'@H_403_136@;
            }
        }
    }
}

695. 岛屿的最大面积

给定一个包含了一些 0 和 1 的非空二维数组 grid 。

一个岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)

示例 1:

[[0,1,0],[0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

示例 2:

[[0,0]]

对于上面这个给定的矩阵,返回 0。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

这道题目和上面的很类似。题目解答如下：

@H_403_136@int maxAreaOfIsland(@H_403_136@null || grid.length <1 || grid[0].length<1@H_403_136@int rx =@H_403_136@int cy = grid[0@H_403_136@].length;
        @H_403_136@int max = 0@H_403_136@int x =0; x< rx; x++@H_403_136@int y= 0;y<cy; y++@H_403_136@if (grid[x][y]==1@H_403_136@) {
                    @H_403_136@int num =@H_403_136@ bfs(grid,y);
                    max =@H_403_136@ Math.max(max,num);
                }
            }
        }
        @H_403_136@ max;
    }

    @H_403_136@int  bfs (@H_403_136@int[][] grid,1)">int x,1)"> y){
        @H_403_136@　　　　　// 每次调用就是一个面积
        @H_403_136@int num = 1@H_403_136@;
        grid[x][y] = 0@H_403_136@;
        Queue<Integer> neQueue = @H_403_136@　　　　　// 这里注意乘以的是col的长度
        neQueue.add(x*cy +@H_403_136@ y);
@H_403_136@　　　　 // 队列不为空
        @H_403_136@neQueue.isEmpty()) {
            @H_403_136@int point =@H_403_136@ neQueue.remove();
            @H_403_136@int nx = point /@H_403_136@ cy;
            @H_403_136@int ny = point %@H_403_136@ cy;
@H_403_136@　　　　　　　// 每一个方向都要判断边界
            @H_403_136@if (nx - 1 >= 0 && grid[nx-1][ny] == 1@H_403_136@) {
                neQueue.add((nx-1) * cy +@H_403_136@ ny);
                grid[nx-1][ny] = 0@H_403_136@;
                num++@H_403_136@if (nx + 1 < rx && grid[nx+1][ny] == 1@H_403_136@) {
                neQueue.add((nx+1) * cy +@H_403_136@ ny);
                grid[nx+1][ny] = 0@H_403_136@if (ny - 1 >= 0 && grid[nx][ny-1] == 1@H_403_136@) {
                neQueue.add(nx * cy + ny-1@H_403_136@);
                grid[nx][ny-1] = 0@H_403_136@if (ny + 1 < cy && grid[nx][ny+1] == 1@H_403_136@) {
                neQueue.add(nx * cy + ny+1@H_403_136@);
                grid[nx][ny+1] = 0@H_403_136@;
            }
        } 
        @H_403_136@ num;
    }
}

广度优先搜索原理与实践深度优先搜索原理与实践（java

概论

基本原理

通用框架

200. 岛屿数量

695. 岛屿的最大面积

参考文章

广度优先遍历（BFS ）（转）

猜你在找的算法相关文章

广度优先搜索原理与实践 深度优先搜索原理与实践（java

概论

基本原理

通用框架

200. 岛屿数量

695. 岛屿的最大面积

参考文章

广度优先遍历（BFS ）（转）

猜你在找的算法相关文章

广度优先搜索原理与实践深度优先搜索原理与实践（java